Cometa afgana (vista anterior)
(Foto: Juan Antonio Muñoz)
La cometa afgana, en general, tiene forma de rombo, casi cuadrada, con una proporción entre sus diagonales de entre 1 a 1,1. Es decir, si D es la diagonal mayor y d es la diagonal menor entonces:
En este caso, la diagonal mayor de mi cometa mide 88 cm
(longitud) y la menor 78 cm (anchura), por tanto la relación entre ambas es de
1,1.
Para construir la cometa he utilizado papel de cometa rojo y
azul de 42 g/m2, bambú, un cordel de algodón, pegamento de barra e
hilo para la brida.
El armazón está construido con varillas de bambú que
previamente había cortado y preparado a partir de una caña de este material,
procurando no eliminar el lado de la corteza para no perder elasticidad. La
varilla vertical se denomina flecha
(diagonal menor) y la varilla horizontal curvada se llama arco (diagonal mayor):
Cometa afgana (vista posterior) mostrando el arco y la flecha
(Foto: Juan Antonio Muñoz)
Hay que tallar el bambú de tal forma que la flecha sea más rígida que el arco. Los bordes del arco se afilan más en los extremos que en el centro para que el arco sea más flexible en los extremos que en el centro.
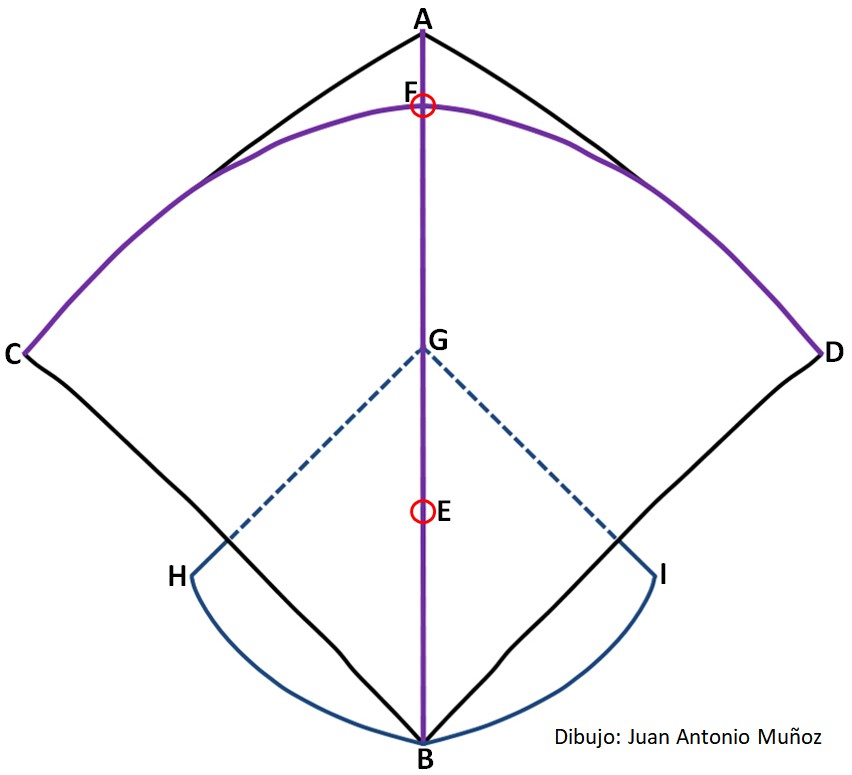
Las dimensiones de los diferentes elementos se indican en el siguiente plano en centímetros, mostrando en color morado las varillas de bambú:
Plano de la cometa afgana
(Dibujo: Juan Antonio Muñoz)
Dimensiones en centímetros:
AB
|
CD
|
AF
|
BE
|
CFD
|
AC, AD
|
CB, DB
|
HG, GI
|
HBI
|
78
|
88
|
8
|
26
|
107
|
56
|
61,5
|
36
|
66
|
La brida va sujeta en los puntos F y E señalados con un círculo rojo en el plano. Su longitud debe ser una vez y media superior a la del arco de la cometa. El punto de amarre de la brida es ajustable mediante un lazo con un nudo Prussik, que permite ajustar la longitud de sus cabos para conseguir el ángulo apropiado de la cometa para el vuelo.
Para ensamblar la cometa, primero se pega el larguero o flecha a la hoja de papel, dejando el lado más rígido de la flecha en la parte superior de la cometa, es decir, en el lado donde se pegará el arco:
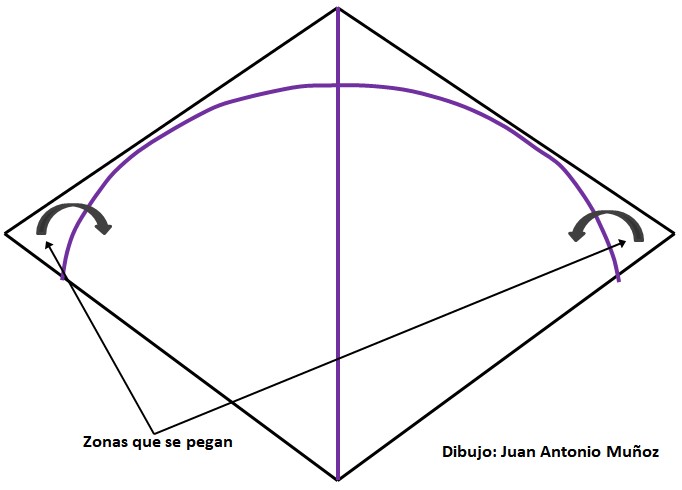
Ensamblaje de la cometa afgana
(Dibujo: Juan Antonio Muñoz)
El arco se coloca curvado sobre el papel de tal forma que su parte superior no sobresalga del papel, como se muestra en la figura anterior. Los extremos del arco y de la flecha pueden sobresalir de la hoja, porque después se podrán cortar las partes que sobresalgan del papel. Nunca se deben cortar el arco y la flecha con las longitudes exactas.
El papel debe ser unos pocos centímetros más grande que el arco en los extremos de la cometa, formando una zona triangular, como se muestra en la figura anterior. Estas partes que sobresalen del arco se doblan y pegan sobre el arco para pegarlas sobre la hoja, tal como indican las flechas curvadas de la figura. En esta operación hay que sujetar firmemente los extremos del arco en su posición para mantener el arco curvado y presionar la parte pegada durante unos segundos para que el pegamento actúe y el papel no se rompa.
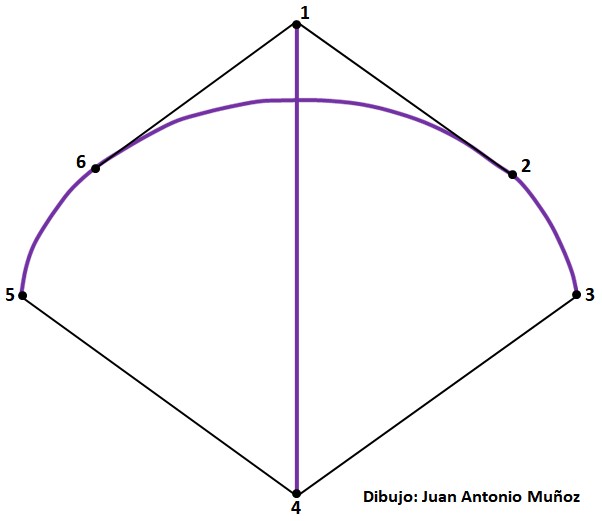
Para formar el perímetro de la cometa se utiliza un hilo ligero, en este caso de algodón. Sobre este hilo se podrá doblar el papel de la cometa formando un dobladillo de unos 5 mm de anchura. Se ata con dos o tres vueltas en cada extremo de la flecha y el arco:
Formación del perímetro de la cometa
con un cordón atado a las varillas
(Dibujo: Juan Antonio Muñoz)
Se puede empezar atando el hilo en el punto 1, enrollarlo alrededor del arco haciendo un nudo en el punto 2, después en el punto 3, y así hasta completar el perímetro en el punto 1 donde se comenzó. Conviene reforzar los nudos con un poco de pegamento para que el hilo no se mueva.
Los extremos de la flecha se refuerzan con piezas de papel pegadas en la parte posterior de la cometa. Para decorar esta última se pegan en la parte anterior unos recortes de papel de diferente color (en este caso azul), en forma de rombo en la punta y ondulados a ambos lados del arco, así como la característica “cola” de la cometa afgana con forma de sector elíptico:
Decoración de la cometa afgana
(Foto: Ana Romero)
Remontando la cometa afgana
(Foto: Ana Romero)
La cometa afgana en vuelo
(Foto: Ana Romero)
Para saber más:
Las cometas en Afganistán
